实用优化算法（六－1）Selection in Genetic Algorithm

14-11-18

Algorithm

algorithm

遗传算法包括三个基本操作选择、交叉、变异，这一篇说说选择（Selection）

##轮盘赌选择（Roulette Wheel Selection）

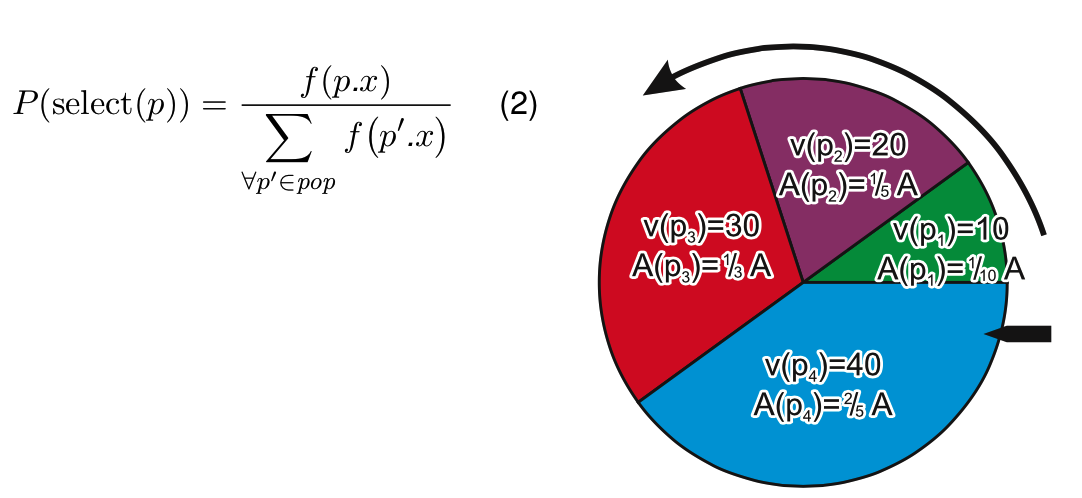
轮盘赌选择法可用如下过程来模拟实现：

1、在［0，1］内产生一个均匀分布的随机函数 r

2、如果 r <= q1，则染色体 x1 被选中。

3、若 qk - 1 < r <= qk (2<=k<=N)，则染色体 xk 被选中，其中qi为染色体xi(i=1,2,…,n)的累积概率，计算公式为：

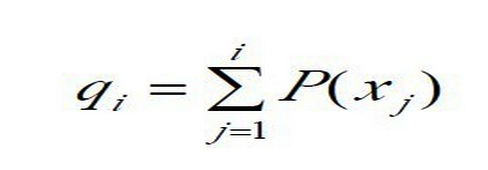
这里我们举一个简单的例子就可以明白累积概率的问题！

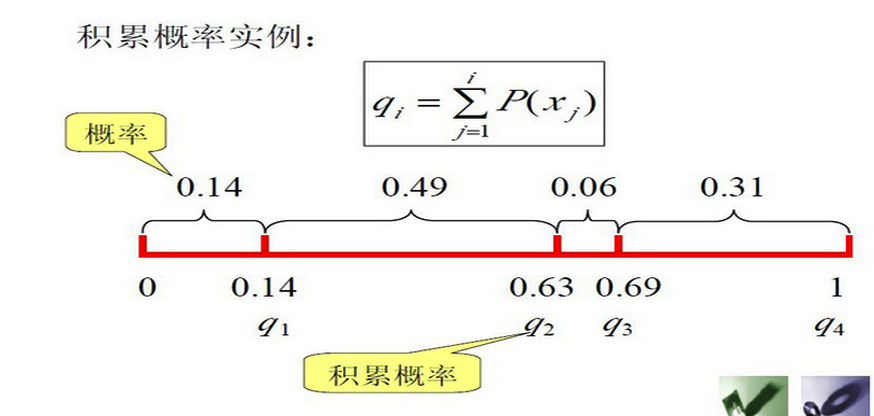
这样我们就可以将所有个体的获取概率均匀分布在[0,1]的范围内，通过生成一个［0，1］的随机数判断它在哪个区间而决定选择对象！

轮盘赌算法的实现步骤：

public class RouletteWheelSelection implements ISelectionAlgorithm {
  private double[] temp;
  public RouletteWheelSelection() {
    super();
  }
  @Override
  public void select(final Individual<?, ?>[] pop, final Individual<?, ?>[] mate, final Random r){
  double[] t;
    double max, last;
    int i, j;
    //将上一次使用轮盘赌算法得到的初始化数组赋值给 t
    t = this.temp;
    //如果是第一次使用轮盘赌选择法或问题空间发生变化，那么初始化 t 和 temp
    if ((t == null) || (t.length < pop.length)) {
      this.temp = t = new double[pop.length];
    }
    max = Double.NEGATIVE_INFINITY;
    //找到个体中适应值最大的
    for (Individual<?, ?> indi : pop) {
      max = Math.max(indi.v, max);
    }
    max = Math.nextUp(max);
    last = 0d;
    //计算每个个体的适应值的累积概率，并存储在数组 t 中
    for (i = 0; i < t.length; i++) {
      last += (max - pop[i].v);
      t[i] = last;
    }
    //确保最大累积概率，个体的累积概率永远不会超过最大累积概率
    t[t.length - 1] = Double.POSITIVE_INFINITY;
    //交配个体选择
    for (i = 0; i < mate.length; i++) {
      //last 中存储了累积概率的总和
      //在累积概率数组 t 中搜索对应值 last * r.nextDouble，如果找到，那么返回对应的索引值
      //如果没有找到并且 last * r.nextDouble 小于 t 中的一个或多个元素，返回一个负数（大于该值的第一个元素的索引的按位求补）
      //如果没有找到并且 last * r.nextDouble 大于 t 中的所有元素，返回一个负数（虽有一个元素索引加1的按位求补），这种情况已经排除在外！
      j = Arrays.binarySearch(t, last * r.nextDouble());
      //选择 last * r.nextDouble 最接近的个体的索引值
      if (j < 0) {
        j = ((-j) - 1);
      }
      //将旋转赌轮盘一次得到的个体纳入交配池
      mate[i] = pop[j];
    }
  }
}

##锦标赛选择（Tournament Selection）锦标赛选择法的原理非常简单，k 个个体竞争一个进入交配池的机会，当然是适应度值最高的个体被选中！

public class TournamentSelection implements ISelectionAlgorithm { // start
  //k 表示从 k 个个体中选择一个进入交配池
  public final int k;
  public TournamentSelection(final int s) {
    super();
    this.k = s;
  }
  @Override
  public void select(final Individual<?, ?>[] pop, final Individual<?, ?>[] mate, final Random r) {
    //交配个体选择
    for(int i = 0; i < mate.length; i++) {
      int a = r.nextInt(pop.length);
      //从 k 个随意选择的个体中选取适应性最强的个体进入交配池
      for(int j = 1; j < k; j++ ){
        int b = r.nextInt(pop.length);
        if(pop[b].v > pop[a].v){
          a = b;
        }
      }
      mate[i] = pop[a];
    }
  }
}

##截断选择（Truncation Selection）截断选择的思想很简单，就是从全部种族个体中选择 mps 个最优秀的个体进入交配池， mps 总是小于种族个体总数 ps。

public class TruncationSelection implements ISelectionAlgorithm {
  public static final TruncationSelection INSTANCE = new TruncationSelection();
  private TruncationSelection() {
    super();
  }
  @Override
  public void select(final Individual<?, ?>[] pop, final Individual<?, ?>[] mate, final Random r) {
    //对 pop 中的所有个体进行排序(默认从小到大-升序排列)
    Arrays.sort(pop);
    //复制 pop 数组中从 0~mate.length 的数据 到 mate 数组中 0~mate.length
    System.arraycopy(pop, 0, mate, 0, mate.length);
}