到现在，我们已经学习了几种不同的优化算法，也许也会有一些解决某些优化问题的经验。对于一些问题，我们或许能够相对容易的找到最佳解决方案，但对于一些其他的问题，也许困难重重。

为什么呢？

对于一些问题（比如：寻找最短路径），有确定的算法能够快速找到最优方案。对于一些其他问题（比如：Partitioning，TSP）结果的好坏完全依赖于我们所使用的算法。

##算法的复杂性

解决TSP问题所花费的时间取决于城市的数量；判断一个数是否是质数取决于该数字的大小。算法完成所需要的 时间/空间 也就是函数输入数据的大小叫做选发的 时间/空间 复杂性。

不同的算法在处理不同难度的优化问题是差别很大，增长速度也不同。

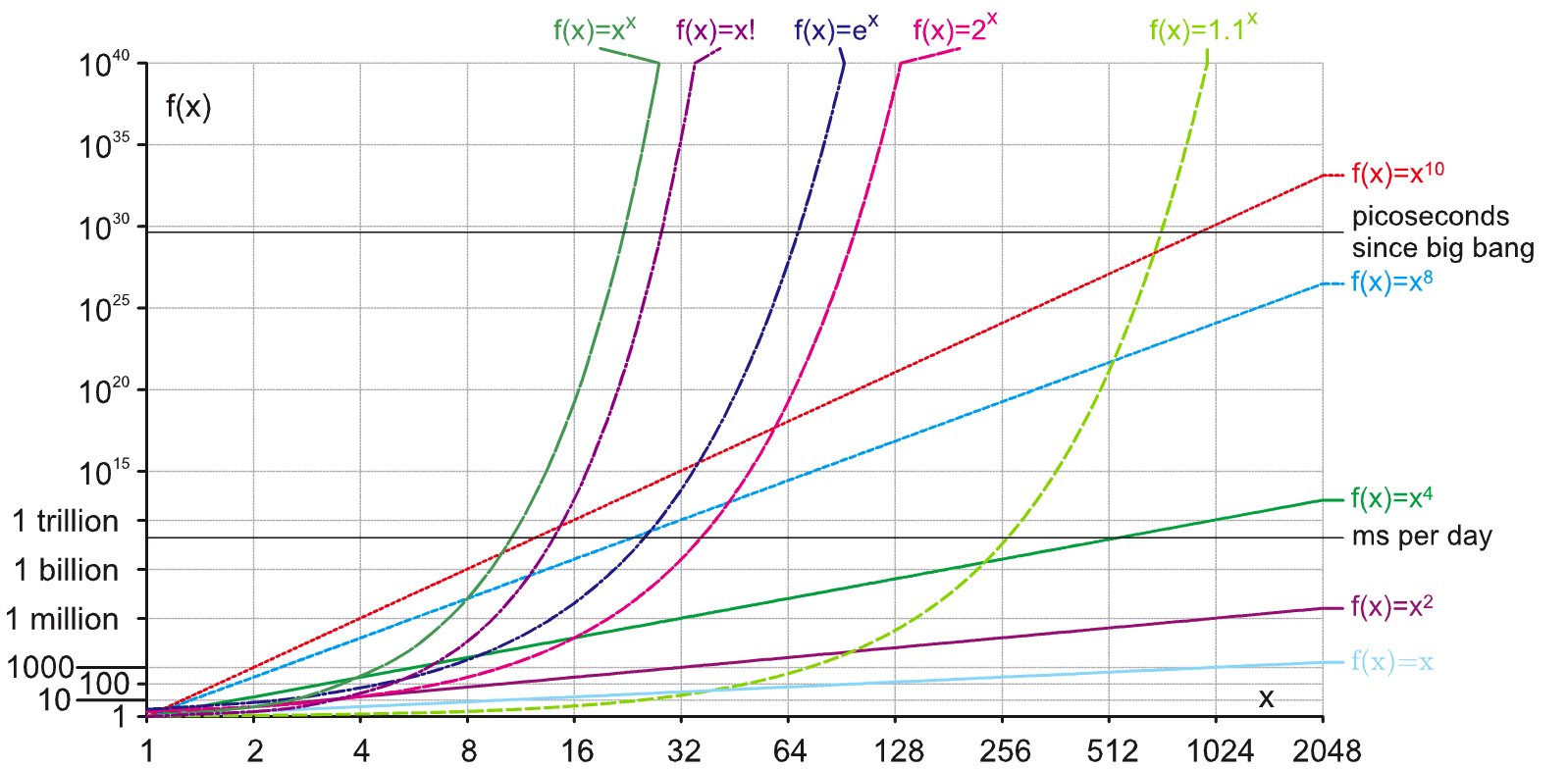
问题的困难：1、解决一个问题所至少需要的时间/资源；2、基于我们所已知的最合适的算法；3、取决于解决问题所使用的机器性能

确定图灵机（Deterministic Tureing Machine）\ 非确定图灵机（Non-Deteministic Turing Machine）

NTMs 可以被 DTMs模拟，但是所需要的步数随着最短接受路径的长度二指数增长

所有能够被 DTM在多项式时间内解决的 属于 class P

所有能够被 NTM在多项事件内解决的属于 class NP

所有真实世界的问题都是 NP-hard 问题： TSP， Constraint Satisfaction Problem， Bin Packing， Vihicle Routing Problem

##令人不满的收敛（Convergence）

让我们暂且先找一个比较接近结果的答案而非准确答案，也不指望去满足全局最优。

问题和算法的什么特征有助于我们得到好的结果？何时我们才能得到好的结构？

收敛（Convergence）：一个优化算法如果不鞥你找打一个新的候选结果或者它只能得到问题空间中的一个很小子集的时候，我们就说它趋于收敛。

多态（Multi-modality）：如果一个函数问题有超过一个最大或者最小的最优结果时就说它有多态性。

Exploitation vs Exploitation：开采（Exploitation）表示在临近区域额搜索好的候选结果；探测（Exploration）表示搜索整个区域。

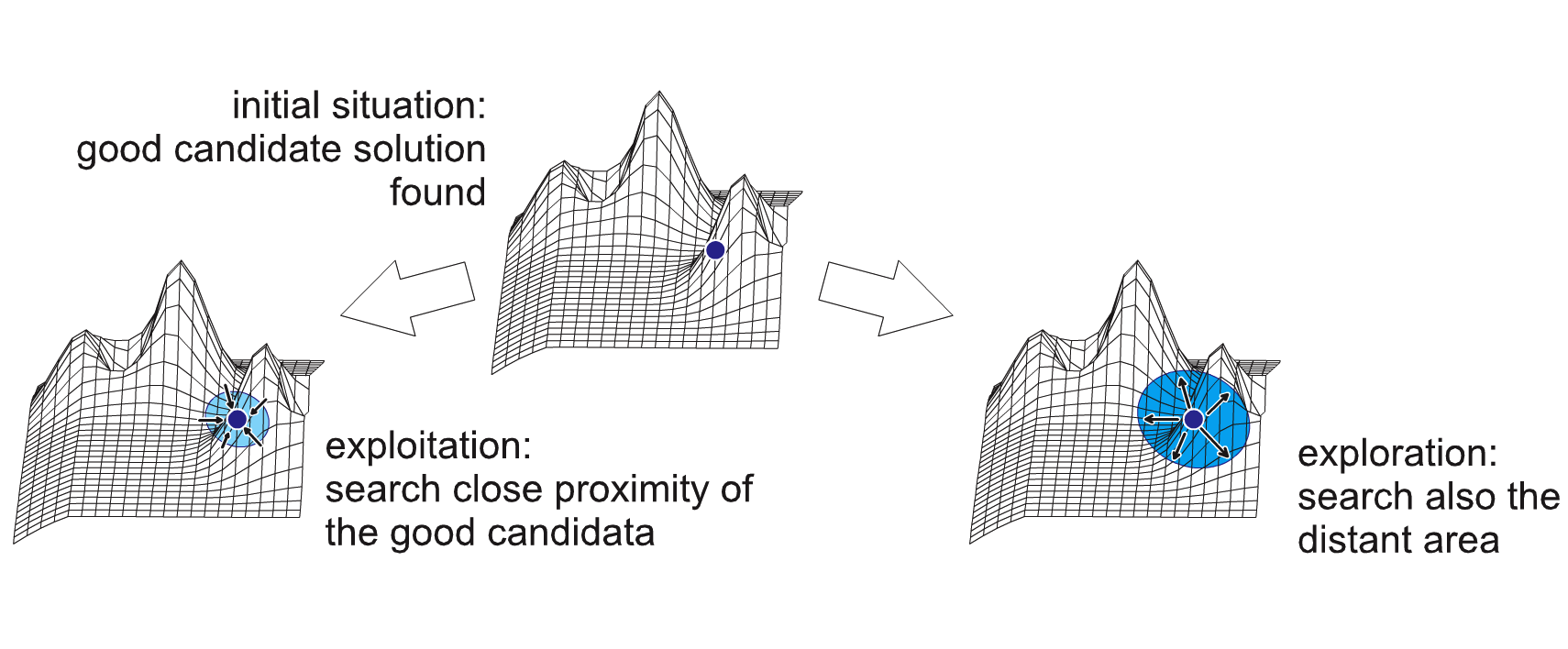
对策：

1、通过平衡exploration 和 exploitation 和 记录不同的候选结果来延迟收敛

2、设计完整的search operators: a) operator 可以从当前的基因型找到其他的基因型 b) 最好在一次搜索操作中完成

3、重启。如果有时总是没有改进，考虑重启算法

4、低选择压力和大的人口基数： a) 允许通过减少压力找到更好的候选结果的方式增加exploration b) 减缓搜索的速度 c) 只是偶尔这样做

5、Sharing ,Niching and Clearing: 给予相似结果更差的适应性标示

6、分类归并候选结果： a) 收集：将数据收集为相似的元素 b) 对人口进行划分，并分类归并 c) 允许人口立刻追踪不同的最佳适应性

7、自适应： 通过改变优化算法的参数来阻止收敛

8、多对象： a) 通过创建一个伪造的目标函数（针对候选结果的某一个特性）将单对象问题转化为多对象问题 b) 通过“Pareto-based优化”来增加差异性

##崎岖性和因果性（Ruggedness & Causality）

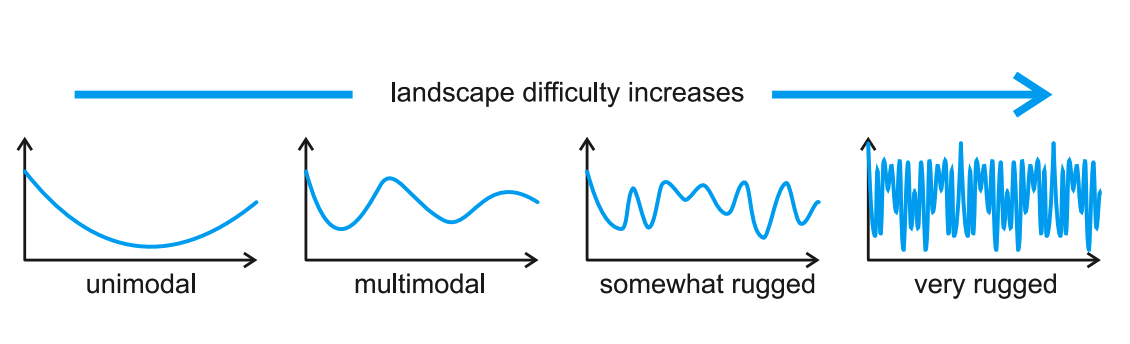
对策：

1、在 EA 算法的杂交过程中使用本地搜索

1) Lamarckian 进化： a) 在基因层面进行 EA ＋ 局部搜索 b) 每一个基因型都是由正常的搜索操作所产生，并且可以精确的使用 HC 的方法 c) 当只关注于局部优化并不纠结于崎岖性讲平稳的得到一个最合适 EA 全图

2) Baldwin 效应 a) 在表现层面进行 EA ＋ 局部搜索 b)每一个表现型都是有GPM映射于基因型所产生的 c) 表现层可以通过 HC 的方法进化 d) 当只关注于局部优化并不纠结于崎岖性讲平稳的得到一个最合适 EA 全局概况

3) Memetic 算法 a) 与Lamarckian和Baldwin相似 b) 搜索操作自己进行局部优化 c) 当只关注于局部优化并不纠结于崎岖性讲平稳的得到一个最合适 EA 全图

4) 其他的杂交方法： 组合 EA 和 HC，或者组合 EA 和 其他机器学习的观点

2、全局近似

1) 尝试修改模型M或者函数的参数让他们的行为与目标函数 f 拥有相同的行为

2) 在这个简单模型上做优化

3) 通过几步操作之后回到目标函数 f 和 最佳结果

4) Update 模型 M， 然后重复以上操作

3、2-，n- 分期优化

1) 第一步，使用慢收敛的优化算法（适合 expliring 整个搜索空间）

2) 接下来使用适合探索当前区域的优化算法 explotation

##迷惑性（Deceptiveness）

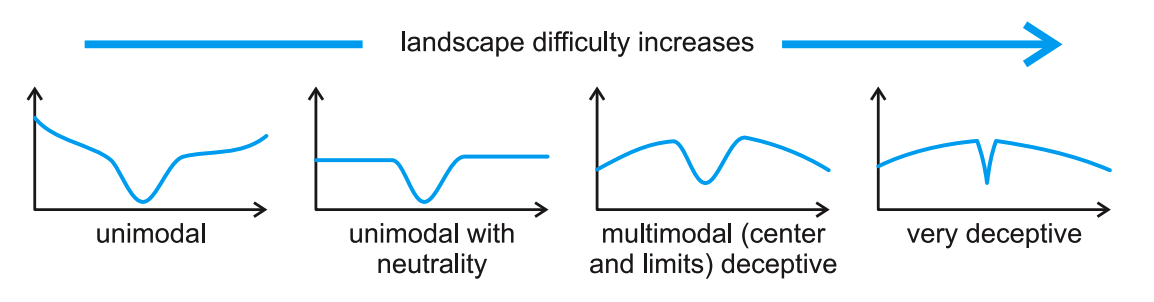
对策：

1、选择合适的代表，可能是组合代表

2、阻止收敛

1）最合适的均匀选择策略

2）新颖的搜索方式

##中立性（nuetrality）

进化性（Evolvability）： 一个优化过程的进化性的当前状态定义为 搜索操作可以找到新的候选结果的可能性

中立网络可以连接搜索空间内不同的区域！

##异位显性（Epistasis）

一个基因能够影响其他基因的表现形式——所有问题的根源

基因的多效性（Pleiotropy）：一个基因负责多个表现型的特性

基因的分离性（Deparability）： 一个函数的 n 个变量可以重写成 n 个函数的和。

通过分离的方式可以很有效的解决可分离的问题（非异位显性问题）

Counrermeasures

1、所有解决崎岖性、中立性、多形态的方法

2、选择合适的表现方式和搜索操作

3、调整参数

4、链接学习 和 变量交互学习

1）找出互相连接的基因

2）将他们作为一个整体来改变

3）例如：在交叉交配的时候，将这些基因绑定起来交换

5、如果是因为异位显性有所限制：写作进化策略

##拓展型（Scalability）

问题所花费的时间随着输入的数据而成指数型增长。

对策：

1、并行性和分布

1）次线性加速

2）并行：使用多喝 CPU 和多线程 GPU

3）分布式：使用联网的多台 PC

2、间接代表1:有生殖力的

1）基因型很小，搜索空间更小，探索会非常容易

2）通过一个简单的 GPM 映射越大，表现性越复杂

3）利用/假设 让表现型更加均匀

3、间接代表2:有发展性的

1）基因型很小，搜索空间更小，探索会非常容易

2）但是GPM会越复杂

3）相比生殖力映射行为更加好

4、探索分离性

1）试图将问题分解为不相关的几个问题，这样搜索空间会小点

2）或多或少的使用分离性来解决问题，通过组合候选结果得到新结果

3）协作进化：使用EA找到如何分解问题的方法

5、同时使用多种算法

##No Free Lunch Theorem 原则

所有算法通过 m 步达到某一个值 y 的概率是相等的。所以并不能绝对的说哪个算法好，哪个个不好。不同算法能够解决不同的问题！

不同的算法适合于解决不同的问题，并不是所有的可能结果都会真实发生在实践中。

• « Previous
• Archive
• Next »