实用优化算法（十四）基因编程（Genetic Programming）

14-12-24

algorithm

algorithm

##什么是基因编程

基因编程是一种进化算法。基于人口的优化算法；过程迭代（每一代）；每一代人口经历适者生存淘汰；被选中的个体通过变异和重组再繁殖

那么与基因算法（Genetic Algorithm）、进化策略（Evolution Strategy）和微分进化（Differential Evolution）的差别是什么呢？

它进化程序或者树结构或者图表结构

##回归符号

给一系列点的集合 S = {(x1, y1),(x2, y2), . . . ,(xn, yn)}

找出函数表达式 ϕ : R → R

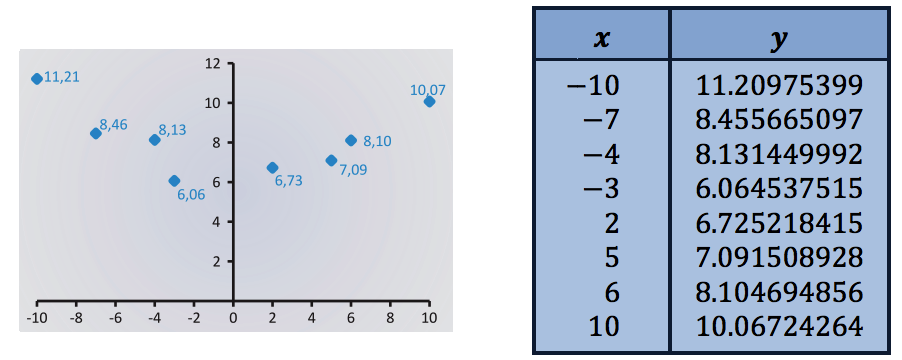
因此我们需要使用基因编程得到回归到符号表达式：

1、使用树结构表现表达式

2、例如 minimize f(ϕ) = Σ (yi − ϕ(xi))^2

3、使用基因编程构造 ϕ

符号复原的思想

一系列点的集合 S = {(x1, y1),(x2, y2), . . . ,(xn, yn)}；

函数集 F = {+，-，*，sin，exp…}

叶子节点集包括变量 x 和实数集 T = {x，R，…}

我们需要找到的是一个有 F、T中元素所组成的一个符合数据的表达式

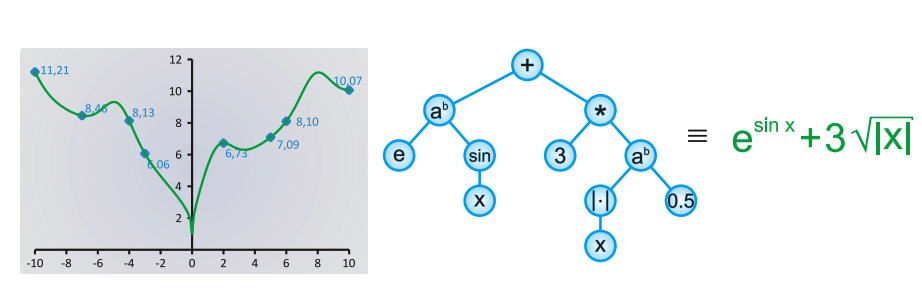
##基因编程

进化算法：

以随机程序开始；

测试个体特征；模拟性能加标准条件（比如：size）；

适应性可以使相关的，决定了其后代的个数；v(ϕ) 符号回归中的适应性可以是，square error f(ϕ) v(ϕ) = f(ϕ) +penalty ∗ size(ϕ)

变异操作是插入一个随机的子树，重组操作是交换子树。

##树的构建

方法一：最大深度构建——添加随机的函数节点到深度 maxDepth-1，最后添加叶子节点

方法二：增长式构建——随机添加函数或者叶子节点，知道所有的树枝都终结，或者达到深度 maxDepth - 1，最后添加叶子节点到所有树枝

方法三：各一半——一半节点采用方法一，一半节点采用方法二

##臃肿（Bloat）

臃肿就是程序无控制的增长

臃肿当然是不好的，高雅的结果总是简单而又小巧，大的程序等于很长的运行时间，运作和评估的增长；大的程序会导致过度的危险；大的程序当然占据很大的内存空间

应对措施：

使用多对象优化；在单对象优化中采取惩罚；设置程序大小的上限；使用特别的变异和交叉操作

##基因编程的实现

public class SymbolicRegressionGP {
  @SuppressWarnings("unchecked")
  public static void main(final String[] args) throws IOException {
    final EA<RealFunction, RealFunction> ea = new EA<>(); // 调用进化算法解决基因编程问题
    final NodeTypeSet<RealFunction> nts;
    final NodeTypeSet<RealFunction>[] binary, unary;
    final IObjectiveFunction<RealFunction> f;

    nts    = new NodeTypeSet<>();			 // 符号集
    binary = new NodeTypeSet[] { nts, nts }; // a binary function has two child elements
    unary  = new NodeTypeSet[] { nts }; 	 // a unary function has only one
    // 自定义添加符号集
    nts.add(new ReflectionNodeType<>(Sin.class, unary)); // we use: sine
    // choose more mathematical operators from package poad.G.trees.data.math
    // and its sub-packages
    // see class oad.examples.lesson_10.SymbolicRegressionGP: it is an example
    // 定义为二叉树
    nts.add(new VariableType(2)); // 2 dimensions!

    f = new SymbolicRegressionObjective(
    	// 在其中添加已知的 输入-输出 对
        new DataPoint(new double[] {/** input values x1, x2*/}, /** measured output y */), //
    );    

    ea.nullary   = new TreeRampedHalfAndHalf<>(nts, 6); // Ramped-Half-and-Half: max depth 6
    ea.unary     = new TreeMutator<>(6);                // the tree mutator: max depth 6
    ea.binary    = new TreeRecombination<>(6);          // binary search operation (crossover)
    ea.ps        = 256;                                 // set population size to some good value
    ea.mps       = 128;                                 // set mating pool size to some good value
    ea.selection = TruncationSelection.INSTANCE;        // use truncation selection
    ea.cr        = 0.3;                                 // set crossover rate to some good value

    for (int i = 1; i <= 100; i++) {           // let's do 100 runs
      ea.termination = new MaxSteps(1000000);  // for each run, allocate 1'000'000 steps
      Individual<RealFunction, RealFunction> res = ea.solve(f); // invoke optimizer

      System.out.println("run " + i + //$NON-NLS-1$
          " has result quality " + res.v + " and result " + res.x.toString()); //$NON-NLS-1$
    }
  }
}