##一些概念 问题的分类：组合问题和数值问题

组合（Combinatorial）优化问题定义在一个有限的离散的问题空间里。比如：位流、元素置换、课程选择等。

数值（Numerical）优化问题定义在数字领域或者涉及实值变量。比如：求的数学方程式、股票预测、飞机机翼设计等。

优化算法（Optimization Algorithm）:优化算法就是找到一个最合适的算法来解决一个优化问题。 算法分为两类：确定算法和随机算法

确定算法（Deterministic Algorithm）:算法的每一步只存在一种方案执行下去，否则算法终止。比如：穷尽枚举法、确定共通启发式算法。

随机算法（Randomized Algorithm）:算法包括至少一种指令要调用随机数。比如：随机举例法、随机本地搜索法（创建一个随机结果，通过每次修改它一点点并判断是否变好了来决定是否保留它）。

有两类随机算法：拉斯维加斯算法（Las Vegas Algorithm）和蒙特卡诺算法（Monte Carlo Algorithm）。拉斯维加斯算法要么返回一个正确的结果要么纯粹没有返回值，蒙特卡洛算法总会终结，它一定会返回一个正确或者错误的结果。

共通启发式演算法（Metaheuristics）:共通启发式演算法是一种解决一般问题的方法。它将目标函数和启发式相结合产生一个抽象并且有效的方式作为一个黑盒程序。

优化算法又可被分为在线（Online）和离线（Offline）两种过程，在线过程需要快速完成，大约在10ms到几分钟的时间内完成。而时间对离线过程并不重要，用户为了得到更好地结果可能要等待几天或者几周时间。

我们将在接下来主要讨论的是有关随机算法、随机本地搜索法、蒙特卡洛算法、离线算法的问题。

##优化结构 接下来，让我们从一个例子开始探讨优化问题：

Example:Traveling Salesman Problem

一个商人选择最短的距离访问 n 个城市。所有的城市只能访问一次并且最终要回到出发的城市。Traveling Salesman Problem(TSP)的目标是要找到一条访问了所有城市并且距离总和最短环路。

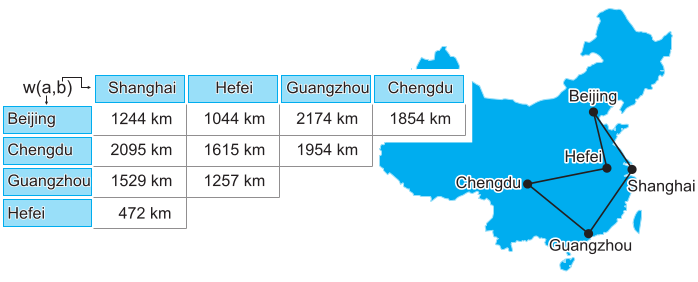
1.问题空间（Problem Space）X: 问题结果x的集合，x被称为备选结果

TSP的问题空间是：X = Π { Beijing , Chengdu , Guangzhou , Hefei , Shanghai }

2.目标函数（Objective Function）f：评判结果是否是最优的函数，X -> R，f(x)是R中的元素，x是X中的元素，如果目标是求最小化,对于f(x1) < f(x2)，表明x1比x2要好。

TSP的目标函数是：Minimize f (x) = dist( Hefei , x[0]) + Σ（i=0->2）dist(x[i] , x[i + 1])+dist(x[3] , Hefei )

这时问题出现了，我们可以尝试遍历所有可能的结果吗？问题空间的大小为X = (n − 1)! / 2，当问题复杂时我们不可能遍历所有结果！！！现在我们并不知道比较好的方案的特征是什么！我们可以计算目标函数f，但不能通过目标函数f求得最小值！那我们现在应该怎么办？

3.共通启发式演算法（Metaheuristics）: 我们知道问题空间X的数据结构，那么我们可以随机创建一个实例x！然后修改已存在的实例x，或者合并存在的实例x1、x2。如果能够足够好的完成这个，我们就成功啦！

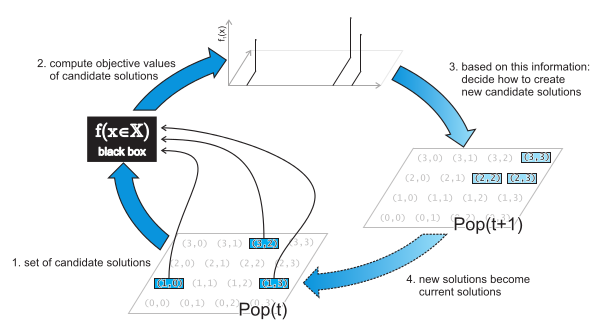
接下来我们就需要得到实例x了！还需要一个修改实例的方法！或者是一个合并实例的方法！

搜索操作（Search Operations）: 通过Nullary Search Operation我们先创建一个G的实例g，然后通过Unary Search Operation修改实例，得到一个新的实例。

通常，我们可以使用著名的数据结构X，比如：Rn ≡ double[]。

那么，TSP的可以将自己的问题空间转化为X = Π { 0 , 1 , 2 , 3 , 4 }

但是如果有些问题的问题空间不是著名的数据结构应该怎么办呢？那我们转化它！比如：

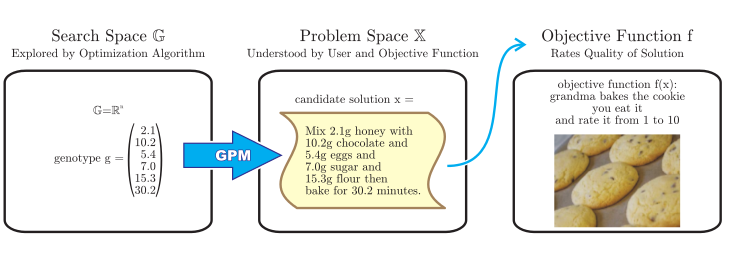
我们把这个过程称为基因-表现型映射（Genotype-Phenotype Mapping），Genotype-Phenotype Mapping（GPM）G → X将实际中的搜索空间（Search Space）G映射到了问题空间X中。

4.终止条件（Termination Criterion）决定了该方法迭代的结束条件，我们通过设置最大步数（MaxStep）来终结算法。

##优化算法函数模型

public abstract class OptimizationAlgorithm<G, X> {
  public INullarySearchOperation<G> nullary;
  public IUnarySearchOperation<G> unary;
  public ITerminationCriterion termination;
  public IGPM<G, X> gpm;
  public final Random random;
  public abstract Individual<G, X> solve(final IObjectiveFunction<X> f);
}

• « Previous
• Archive
• Next »