实用优化算法(二)Hill Climbing
- 14-10-12
- Algorithm
- algorithm
上一篇我们学习了共通启发式演算法:从一个(或多个)初始的一般性候选结果开始,迭代修改(或合并)候选结果。
我们应该如何最简单的实现这个思想呢?
##登山算法
登山算法(Hill Climbing Algorithm): 是一个解决优化问题的局部搜索算法,通过不停地迭代从一个候选结果向另一个候选结果“移动”直到终止条件满足。
public class HC<G, X> extends OptimizationAlgorithm<G, X> {
public HC() {
super();
}
@Override
public Individual<G, X> solve(final IObjectiveFunction<X> f) {
Individual<G, X> best, pnew;
best = new Individual<G, X>();
pnew = new Individual<G, X>();
//随机创建候选结果best,并将其初始化为当前最优结果
best.g = nullary.create(this.random);
best.x = this.gpm.gpm(best.g);
//由Termination函数决定终止条件
while(!(this.termination.shouldTerminate())){
//修改当前最优结果best,并将其传递给新的候选结果pnew
pnew.g = this.unary.mutate(best.g, this.random);
pnew.x = this.gpm.gpm(pnew.g);
pnew.v = f.compute(pnew.x);
//通过目标函数f比较修改后的pnew是否比best好一点
//如果比修改前好,那么将当前其赋值给当前最优结果best
if( pnew.v <= best.v){
best.assign(pnew);
}
}
//返回最优结果
return best;
}
}
##登山算法存在的问题
登山算法每次都通过搜索空间朝一个更好地候选结果“移动”。那么每次都朝一个更好的方向移动会发生什么问题呢?
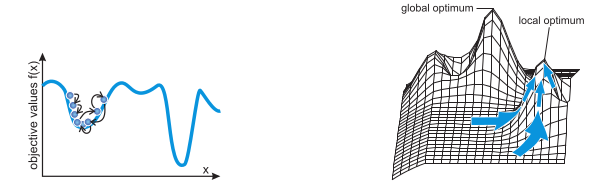
通过上图我们可以看到: 如果不能够探索搜索空间内的其他部分,优化算法会过早的朝一个局部优化融合。在空间内的其他部位会有更有的结果我们将无法找到!
##总结
现在我们已经实现了一个简单的共通启发式演算法!它好吗?这个问题我们将在后面探讨!