实用优化算法（四）Simulate Annealing

14-10-18

Algorithm

algorithm

在第二篇我们介绍了登山算法，并说明了它为什么是一个局部优化算法！这一节我们将介绍”模拟退火算法“，它将通过一些方式来避免过早趋于局部优化的问题，让我们开始吧！

##“退火”（Annealing）介绍

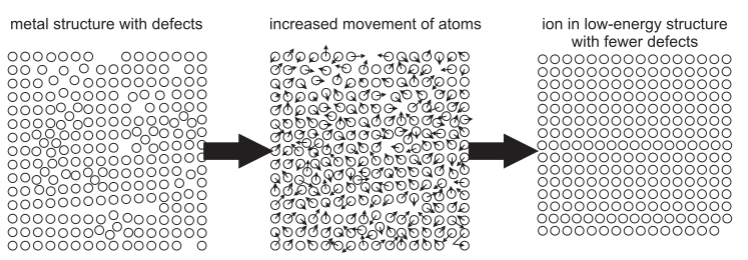
金属的冷加工会导致晶体结构的缺陷，于是在冷加工之后，会来一次退火。当金属加热到大概0.4个冶炼温度的时候金属内部的离子就开始到处移动。当金属慢慢冷却下来，离子的变得低能，稳态——金属变得更加稳定。在这个过程中，离子会暂时的处于高能状态，最后，不稳定的结晶态会经过一系列变化成为一个更稳定的结构。

##梅特罗伯利斯算法（Metropolis Algorithm）

梅特罗伯利斯想要以蒙特卡洛算法的方式模拟退火这个过程

一些参数 ：温度（T）随时间降低; 能量状态（E），离子移动的越快，能量越高，E越大; pos是当前的离子状态，pos’是一个新的状态。

∆E = E(pos’) - E(pos)

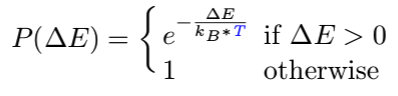
P（∆E）表示新装态pos’可能被接受的一个概率。

Metropolis Algorithm表现了物理系统是如何找到一个低能状态的。而这个物理系统正好可以随着时间的变化接受一个更加糟糕的结果，从而避免了“局部优化”！这或许正好就是登山算法（Hill Climbing）过早收敛的问题的补救办法！

模拟退火算法 = 登山算法 + 依据梅特罗伯利斯方法有时接受一些比较糟糕的状态

##模拟退火算法（Simulate Annealing）

∆E = f (x’) − f (x) ： ∆E表示新状态（x’）和候选结果（x）的差值

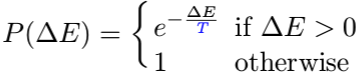
P（∆E）表示新的候选值 x’ 能够被采纳的概率。 T 温度随着时间的增加而减少

public class SA<G, X> extends OptimizationAlgorithm<G, X> {
  /** the temperature schedule to use */
  public ITemperatureSchedule temperature;
  /** instantiate */
  public SA() {
    super();
  }
  /** {@inheritDoc} */
  @Override
  // end
  public Individual<G, X> solve(final IObjectiveFunction<X> f) {
  	Individual<G, X> pnew, pcur, best;
  	//_e表示新的候选结果 x 和旧的候选结果的 x' 差值
  	double _e, T;
  	pnew = new Individual<G, X>();
  	pcur = new Individual<G, X>();
  	best = new Individual<G, X>();
  	pcur.g = this.nullary.create(this.random);
  	pcur.x = this.gpm.gpm(pcur.g);
  	pcur.v = f.compute(pcur.x);
  	best.assign(pcur);
  	int t = 0;
  	while(!(this.termination.shouldTerminate())){
	  pnew.g = this.unary.mutate(pcur.g, this.random);
	  pnew.x = this.gpm.gpm(pnew.g);
	  pnew.v = f.compute(pnew.x);
	  _e = pnew.v - pcur.v;
	  //当新的候选结果比当前结果更优时
	  if( _e <= 0 ){
	  	  //收录新结果
		  pcur.assign(pnew);
		  //比最佳结果更优时，将其替换为最佳结果
		  if( pcur.v < best.v ){
			  best.assign(pcur);
		  }
	  }
	  //关键点！在这里偶尔接受比较糟糕的状态
	  else{
	  	  //随着时间t的增加，调用getTemperatrue函数取得随时间 t 增加正在降低的温度 T
		  T = temperature.getTemperature(t);
		  if(Math.random() < Math.exp(-(_e / T))){
		  	  //随机数小于 P（∆E） ，接受新状态作为当前状态
			  pcur.assign(pnew);
		  }
	  }
	  //退火时间随着迭代的次数增加
	  t += 1;
  	}
  	return best;
  }
}

##温度调控

温度调控可以让模拟退火算法（Simulate Annealing Algorithm）的表现行为从“随机行走算法（Random Walking Algorithm）”的高温状态（T越大P（∆E）越大，糟糕的状态被接受的可能性就越大）转向“登山算法（Hill Climbing Algorithm）”的低温状态（T越小，糟糕的状态被接受的可能性就越小）。

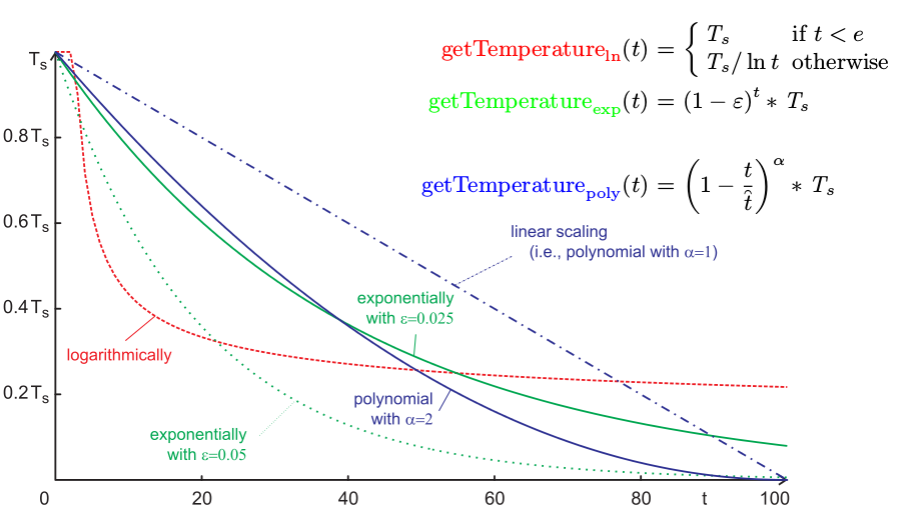
对数调度（Logarithmic） : 参数Ts的取值要比“本地最小目标差值”和“最佳临近候选结果”的值要大。

指数调度（Exponential） : 通过实验来决定 ε ∈ (0, 1)。

多项式调度（Polynomial） : α 是固定的，为1， 2 或者 4；当超过迭代的限定值t时，T 应该等于 0.

适应性调度（Adaptive） : 每 m 步，T = β ∗ (f (p cur . x) − f (x))， β由实验决定。

##结论

如果温度 T 可以缓慢的减少，不同优化实验证明结果可以收敛到全局最优。

快速降温调度会导致不能保证收敛情况，但是进程将会加快很多。