##前言 我们已经学习了好几种算法了(登山算法、随机行走算法、随机采样算法、模拟退火算法)。当我们遇到一个优化问题时，我们应该采用哪种算法来解决它呢？

1、随机算法的性能并不能完全确定！每一次运行算法去解决一个问题时都是与之前的运行过程是相对独立的，并且每次结果都不同。

2、只执行一次算法并不能得到可信的信息。静态评估一组运行结果是完全有必要的。

##性能指标 两个关键参数 ： 在一定数目的性能评估后所达到的最好目标值； 达到一个特定的目标值所需要的性能评估次数。

绝对运行时间：将运行时间精确到ms

优点 ： 工作汇报中结果格式相同；定量才能有所意义；包括了许多“隐藏复杂性”的算法等。

缺点 ： 强依赖于机器； 在10ms的时间粒度里面发生了许多事情，不仅仅是算法的运行；容易被外界因素干扰（比如：操作系统、调度方式、其他的进程、I/O、交换空间等）

函数评估（FEs）:测量完整结构和测试候选结果的数目

优点 ： 汇报结果格式相同；设备无关性；不会被“外间因素”影响；许多优化算法计算目标结果的过程是一个耗时的任务。

缺点 ： 与真实时间无关；并不包括“隐藏复杂性”的算法；在不同情况下代价不同。

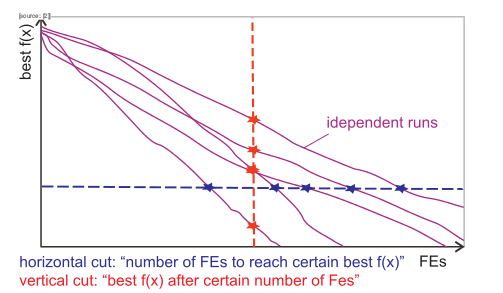
水平线 ： 表示要达到一个特定的目标值所需要的性能评估(FEs)次数。

垂直线 ： 表示在一定数目的性能评估后所能达到的最好目标值。

（没有官方舆论表示哪一个关键参数更好，完全依据具体情况判断，最好从两方面同时评估一个算法）

##统计方法 重要的区别：“样本（Sample）”表示我们测量的对象；“分布（Distribution）”表示理想过程的一个渐进结果。

分布情况统计参数都是从一个样本中估算出来的。

算术平均（Arithmetic Mean） ： 是一个期望值的预期。

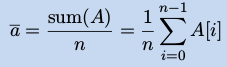
中位数（Median） : 中位数 X 是样本和分布最中间的数。

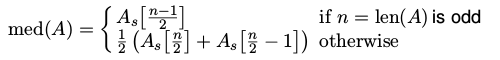
Mean vs. Median : 在描述一个随机过程时，我们应该总是使用中位数而不是算数平均数。因为中位数是对异常值适用性强,算术平均数只适用于对称分布，对偏斜分布的描述很糟糕。

标准差（Standard Deviation） :

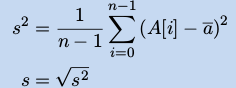
位数（Quantiles） : q 位分割数据样本A = (A[1] , A[2] , . . . , A[n])为 q 份，每一部分元素数目相等（A为顺序样本，且序号从 0 开始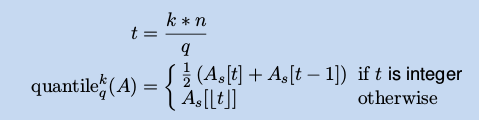） （2-位就是中位数， 4-位就是四分位）

例子：

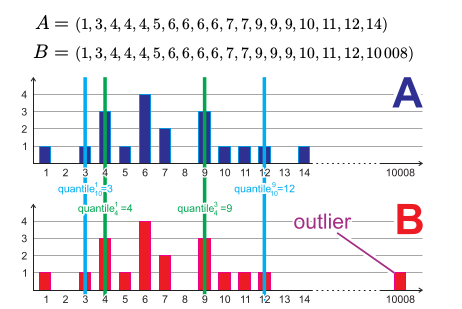
Standard Deviation vs. Quantiles : 标准差总是适用于对称分布，位数总是对异常值和偏斜分布适用性更强。

健壮的统计方法是 ： 中位数（Median）和位数（Quantiles）,如果有必要，再计算算术平均数和标准差。

##统计比较 我们通过将两种不同的优化算法分别运行20次来比较它们的优劣，两个中会有一个得出的结果好一点。断言“A算法要比B算法好一点”，是在有确定概率 α 错误的情况下得到的。

比较两个数据集合A = (a1 , a2 , . . . ) 和 B = (b1 , b2 , . . . )，它们取自两个分布Da和Db，采用某种统计学方法γ，就γ而言，我们假设Da和Db是不同的（假设H1），相反的假设为γ(a) = γ(Db)（假设H0）,如果p小于某个有意义的水平值α（通常是1%或者2%），那么我们可以反对假设H0接受假设H1了

一个特别的例子

A = (2, 5, 6, 7, 9, 10) B = (1, 3, 4, 8)

统计学操作γ ,我们选择算数平均数。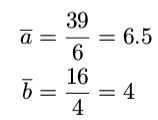

问题是：A和B的算数平均数的差别保持在α = 2%吗？

零假设H0为：A和B来自同一个过程，它们的差别是因为随机取样的缘故。

如果过A和B来自同一个分布，那么我们会有一个大的样本集合O = A ∪ B = (1, 2, 3, 4, 5, 6, 7, 8, 9, 10)，任何将其分割为4、6两份的操作都有相同的概率。从结合O中选择6个样本有210中可能性，通过实验我们发现一共有27个组合的算数平均数小于或等于4，那么假设H0成立的概率是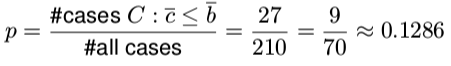，从另外一个方向入手我们同样可以得到相同的结论。

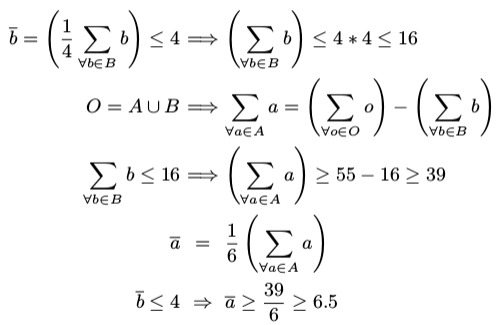
因此，如果我们要声称A和B来自两个不同的分布，那么我们错误的概率就是p ≈ 0.13 。 在α = 2%的前提下（2% < 0.13），说明A和B来自于同一个分布。

• « Previous
• Archive
• Next »