进化策略是对于数值优化问题的进化算法，搜索空间是实数向量 G = Rn . 这种进化方式有不同的人口处理方式，将变异作为主要的搜索操作（Search Operation）。

主要的思路是：自适应搜索——搜索操作自动优化，根据搜索的过程不断调整。包括内因和外因的策略参数。

##人口处理（Population Treatment）

进化策略采用的是截断算法。有两个人口数目相关的参数—— λ：后代的数目 μ：交配池的大小

(μ + λ)算法：

λ个后代由 μ 个父代产生

λ个后代和 μ 个父代共同构成新的人口总体 ps = μ + λ

只有 ps 中适应性最强的 μ 个个体存活

父代也可能存活：持续／稳定状态的方法

(μ，λ)算法：

λ (>= μ) 个后代由 μ 个父代产生

在 λ 个后代中，只有 μ 个适应性最强的活下来

所有的父代都被丢弃：灭绝／分代 EA

(1+1)-ES: Hill Climbing; (1,1)-ES: Random Walk

(μ/ρ + λ):

(μ + λ)进化策略带有 ρ－ary 繁殖操作

ρ ＝ 每个子代所拥有的父代的个数

默认：ρ ＝ 1（变异）；ρ ＝2（交叉法交配）

(μ/ρ , λ):

(μ, λ)进化策略带有 ρ－ary 繁殖操作

在 μ 个子代中，只有 λ 个适应性最强的活下来

##选择法

在（μ ＋ λ）和 （μ，λ）算法中，只有 μ 个适应性最强的个体存活，在进化策略中，我们就选用截断算法（truncation Selection）

如果不了解截断算法，请查看实用算法(六-1)Selection in GA

##变异

变异和选择是ES算法的主要操作。

大多数ES:（1+1）并没有重组操作，假设搜索空间G和解决空间X是相同的（我们就不需要GPM了）。

让我们假设搜索空间是一些实数， X＝ G＝ R，ES中通过从正态分布（μ = x）中产生一个新的样本替换的方式变异一个实数 x ∈ R

变异操作的参数：以正态分布的标准差 σ 作为步长

目标函数通常是 n 维并且有不同的特征：

1、对称并且是关于轴平行

2、也许是集中于某一个轴并且关于轴平行

3、也许是过分集中并且不关于轴平行

变异：我们想能够创建符合以上这些形状的新候选结果

那么通过 n 维正态分布取样来实现，有三种不同的方式来定义这样的分布，三种方式参数不同

对于这些参数，标准差，ES可以使用：

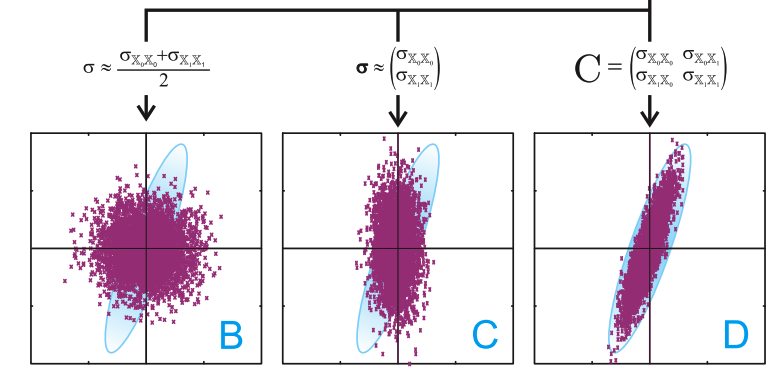
B、一个标准差参数 σ 用于所有结果向量中每个元素（我们仅仅使用 n 次全局正态分布）

C、用于标准差 σ 的向量用作基因型每一个元素的一个值

D、一个写方差矩阵 C 用于转换二进制交流的基因

使用 B 方法,但一直标准差作为变异步长 p.w = σ

public double[] mutate(final double[] genotype, double sigma, final Random r){
  final double[] g = genotype.clone();
  double x;
  for(int i = 0; i < g.length; i++){
  	do{
  	  x = genotype[i] + sigma * r.nextGaussian();
  	}while(x < this.min || x > this.max);
  	g[i] = x;
  }
  return g;
}

##自适应（Self-Adaptation）

进化策略是自适应的：变异操作的参数随时间改变

变异步长－记住HC 实数优化的例子：

1、大步长：开始高速提升，后来缓慢提升

2、小步长：开始低速，偶尔高速，然后又进入低速

3、这个就是 exploration vs exploitation 的困境

并不是根据返回值确定一个固定的步长，而是让优化算法随时间适应步长

要么是内因（在个体中编码并进化他们）或者是 外因（维持整个人口）

##The 1/5th Rule

假设使用方法B，单一标准差作为变异正态分布的步长

想法：根据搜索是否成功适应这个步长

使用基本算法：（1+1）－ES HC？

两个关键参数需要测量： 1、变异操作的成功概率 Ps

2、进程比率 φ,（期望距离）

The 1/5th Rule: 为了获得（1+1）－ES等方性变异的最佳局部优化性能，通过将成功概率 Ps 的值设定为大概 1/5 来调整变异强度 σ

随着 σ 的升高,Ps单调的减少（limσ→0 PS = 0.5 to limσ→+∞ PS = 0）

1、如果成功概率Ps > 0.2，增加变异强度 σ（加快优化进程）

2、如果接受变异的部分比率低于 0.2，那么因为步长太长了而 σ 必须需要减少

优点（Advantages）: 如果许多变异都是成功的——那么我们可以加大步长让进程加快

如果许多变异都未成功——那我们缩小步长以便我们可以接近最优结果而不是跳过它

探索与开发的平衡

缺点（Ddrawbacks）: 很容易的趋向于过早收敛

对于 (1+1)-ES：没有利用人口的概念

只有单一参数 σ：对于不同的规模或者规模之间的相关性不能够模型化步长。

只有单一参数 σ：不能够较简单的拓展到基于人口的方法中

下面我们将具体展示 （1+1）－ES 的进化方法。

public class ES1P1<X> extends OptimizationAlgorithm<double[], X> {// start
  public double a;//步长的乘数
  public double sigma0;//初始的 sigma,变异强度
  public int L; //适应频率
  public ES1P1() {
    super();
  }
  @Override
  // end
  public Individual<double[], X> solve(final IObjectiveFunction<X> f) {
    Individual<double[], X> best, pnew;

    best = new Individual<double[], X>();
    pnew = new Individual<double[], X>();

    best.g = this.nullary.create(this.Random);
    best.x = this.gpm.gpm(best.g);
    best.v = f.compute(best.x);

    pnew.assign(best);

    int t = 1;//迭代次数
    int s = 0;//成功次数
    double ps = 0;

    while(!(this.termination.shouldTerminate())){
      pnew.x = this.gpm.gpm(pnew.g);
      pnew.v = f.compute(pnew.x);
      if(pnew.v <= best.v){
      	best.assign(pnew);
      	s = s + 1;//成功一次
      }
      //每 L 次迭代后，开始自适应
      if(t % L == 0){
      	ps = s / L;//计算成功概率
      	if(ps < 0.2){
      	  //成功概率偏低，减少buchang
      	  sigma0 = sigma0 * a;
      	}
      	else if(ps > 0.2){
      	  //成功概率高，加快优化进程
      	  sigma0 = sigma0 / a;
      	}
      	s = 0;//成功次数归零
      }
      //根据新得到的 sigma0 来进行变异
      pnew.g = this.unary.mutate(best.g, sigma0, this.random);
      t = t + 1;
    }
    return best;
  }
}

其中的变异方式为：

public double[] mutate(final double[] genotype, double sigma, final Random r){
	final double[] g = genotype.clone();
	double x;
	for(int i = 0; i < g.length; i++){
		do{
			x = genotype[i] + sigma * r.nextGaussian();	
		}while(x < this.min || x > this.max);
		g[i] = x;
	}
	return g;
}

##内因参数（Endogeneous Parameters）

并不是只有一个中心化的外因策略参数

在进化策略中对于每一个个体创建一组参数

个体记录是由celuecanshu编码的信息 p.w 拓展的

策略参数现在更像是一组基因－内因

p.w 如果应用到个体 p 时可以作为变异的步长

信息p.w 进过繁殖羽基因型 p.g∈ G 变的相似

作为选择的主体，好的策略参数将会发现好的候选结果

##重组（recombination）

离散重组：对 ρ（父代的个数） 实数向量联合交叉的延展，如果 ρ = 2 ，返回父代创建的杂交立方的一角

中间体重组：对 ρ 实数向量的权重平均交叉的延展，返回有父代创建咱家里放的一个内部点

##参数繁殖

内部参数的繁殖

1、重组策略参数 p.w：中间体重组

2、与基因型的变异不同：我们变异->变异的强度

3、变异意味着改变决定哪个候选结果应该变异

4、在这里 完全值（1、7、1.5）并不有趣

5、但是规模更大，1、10、0.1、10000、0.001

6、于是我们关心的是规模

7、正态分布在它的中心产生近似相等规模的值

8、对数正态分布产生不同规模的值

9、变异的策略参数：使用对数正态分布变异

##CMA-ES

协方差矩阵自适应进化策略——Covariance Matrix Adaptation Evolution Strategy(CMA-ES)是针对连续实数域的极为强有力的优化方法。

对于崎岖、非连续、形状弯曲或者局部优化等都运行良好。

原则：

每一代新的子代是从多变量的正态分布函数中去养而来的，于 变异的D方法相似，允许表示第二级联系。

父代是通过截断选择法选出来的。

新的人口是从正态分布中取样而来的，父代个体完全被遗弃。

• « Previous
• Archive
• Next »