实用优化算法（十三）解决UglyFunction问题

14-12-22

algorithm

algorithm

##介绍 最小化丑陋的函数式问题：有一个在实数[-10,10]^10 十维空间的丑陋函数式，我们的目标是要找到它的最小值。换句话说，我们需要找到一个十维向量 x，可以让函数 f(x) 得到一个最小的可能结果。

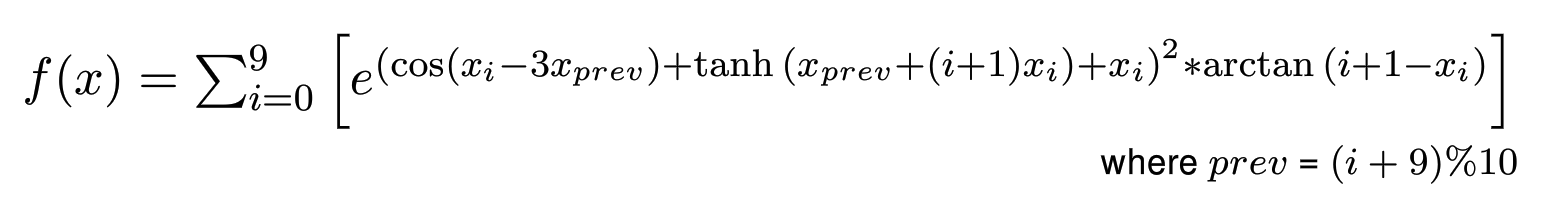
今天，我们就是尝试使用多种方法解决 UglyFunction 问题。

慢着，我们似乎已经学过进化策略，对于数值问题，我们是不是应该使用进化策略中的一些方法呢？！

问题空间：Rn [-10,10]^10

目标函数：既是UglyFunction本身

##使用HC解决UglyFunction

GMP：使用登山算法基因型与表现型完全相同

搜索操作：

Nullary:初始化候选结果

public final class RnNullaryUniform extends Rn implements INullarySearchOperation<double[]> {// start
  public RnNullaryUniform(final Rn def) {
    super(def);
  }
  @Override
  public final double[] create(final Random r) {
    final double[] g = new double[this.dim];
    //随机构建一个长度为10的数组（候选结果为10维向量）
    for (int i = g.length; (--i) >= 0;) {
      //将每个元素随机赋值为 -10~10 的双精度浮点数
      g[i] = (this.min + (r.nextDouble() * (this.max - this.min)));
    }
    return g;
  }
}

Unary：变异候选结果

public class RnUnaryNormal2 extends Rn implements IUnarySearchOperation<double[]> {
  public RnUnaryNormal2(final Rn def) {
    super(def);
  }
  @Override
  public double[] mutate(final double[] genotype, final Random r) {
    double d;
    final double[] g = genotype.clone();
    for (int i = g.length; (--i) >= 0;) {
      //使用进化策略中的正态分布变异 B 方法
      do {
        d = (g[i] + (r.nextGaussian() * (this.max - this.min) * 0.01d));
      } while ((d < this.min) || (d > this.max));
      g[i] = d;
    }
    return g;
  }
}

调用HC解决UglyFunction：

public static void main(final String[] args) throws IOException {
  final HC<double[], double[]>    hc      = new HC<>();         // create HC
  final UglyFunction              problem = new UglyFunction(); // the problem/objective
  //Rn 表示了在 -10~10 之间，维度为 10
  final Rn                        rn      = new Rn(-10d, 10d, 10);
  //定义搜索操作
  hc.nullary     = new RnNullaryUniform(rn); // instantiate nullary search operation
  hc.unary       = new RnUnaryNormal2(rn);   // instantiate unary search operation
      
  for (int i = 1; i <= 100; i++) {          // let's do 100 runs
    hc.termination = new MaxSteps(1000000); // for each run, allocate 1'000'000 steps
    Individual<double[], double[]> res = hc.solve(problem); // invoke optimizer
    System.out.println(res.v + " from " + Utils.toString(res.x));
  }
}

##使用EA解决UglyFunction

Search Operations:

Nullary:随机生成 dim*40 的二进制流数组

Unary:随机选择一位翻转该值

binary:使用组合式交叉法

调用EA：

public class EAOnUglyFunction {
  public static void main(final String[] args) throws IOException {
    final EA<boolean[], double[]>      ea      = new EA<>();         // create EA
    final UglyFunction                 problem = new UglyFunction(); // the problem/objective
    final Rn                           rn      = new Rn(-10d, 10d, 10);
    
    ea.nullary     = new BitsNullaryUniform(rn.dim*40); // 初始化nullary搜索操作
    ea.unary       = new BitsUnaryFlip();               // 初始化unary搜索操作 (变异)
    ea.binary      = new BitsBinaryUX();                // 初始化二进制搜索操作（交叉）
    ea.ps          = 48;                                // 设置人口基数
    ea.mps         = 16;                                // 设置交配池的大小
    ea.selection   = TruncationSelection.INSTANCE;      // 选用截断算法
    ea.gpm         = new BitsToDoublesGPM(rn);          // 使用双精度浮点数到二进制位流的映射方法
    ea.cr          = 0.3;                               // 设置交叉概率为 0.3
    
    for (int i = 1; i <= 100; i++) {                           // let's do 100 runs
      ea.termination            = new MaxSteps(1000000);       // for each run, allocate 1'000'000 steps
      Individual<boolean[], double[]> res = ea.solve(problem); // invoke optimizer
      System.out.println(res.v);
    }
  }
}

##使用ES解决UglyFunction

Search Operations:

Nullary:随机生成长度为10的值的大小在 -10~10 之间的双进度浮点数。

Unary: 根据参数列表中的 sigma 使用进化策略的变异法即：x = genotype[i] + sigma * r.nextGaussian()

调用ES解决UglyFunction：

public class ESOnUglyFunction {// start
  public static void main(final String[] args) throws IOException {
    final ES1P1<double[]> es      = new ES1P1<>();      // create ES
    final UglyFunction    problem = new UglyFunction(); // the problem/objective
    final Rn              rn      = new Rn(-10d, 10d, 10);
        
    es.nullary       = new RnNullaryUniform(rn); // instantiate nullary search operation
    es.unary         = new RnESUnaryNormal(rn);  // 正态分布变异法
    es.a 			 = 0.95;					 // 设置变异强度变化的步长乘数为 0.95
    es.L 			 = 50;						 // 设置每50次迭代后进行一次适应性调整
    es.sigma0 		 = 5;						 // 设置初始化变异强度为 5
        
    for (int i = 1; i <= 100; i++) {           // let's do 100 runs
      es.termination = new MaxSteps(1000000); // for each run, allocate 1'000'000 steps
      Individual<double[], double[]> res = es.solve(problem); // invoke optimizer
      System.out.println("run " + i + 		//$NON-NLS-1$
          " has result quality " + res.v + 
          " and result " + Arrays.toString(res.x)); //$NON-NLS-1$
    }
  }
}

##使用DE解决UglyFunction

public class DEOnUglyFunction {
  public static void main(final String[] args) throws IOException {
    final DE<double[]> de         = new DE<>();      // create ES
    final UglyFunction    problem = new UglyFunction(); // the problem/objective
    final Rn              rn      = new Rn(-10d, 10d, 10);
        
    de.nullary     = new RnNullaryUniform(rn); 
    de.ternary     = new RnRecombineDE(rn,0.5); // 设置三元组合方法
        
    for (int i = 1; i <= 100; i++) {           // let's do 100 runs
      de.termination = new MaxSteps(1000000); // for each run, allocate 1'000'000 steps
      Individual<double[], double[]> res = de.solve(problem); // invoke optimizer
      System.out.println("run " + i + //$NON-NLS-1$
          " has result quality " + res.v + 
          " and result " + Arrays.toString(res.x)); //$NON-NLS-1$
    }
  }
}